教
材
作
家
<第1回>やさしい星の書き方 正五角形と黄金のL(エル)

今回の教材は、黄金のL(エル)です。

それは、こんな形をしています。
教材作家にとって「教材」とは、「もっていくもの」という意味です。
遠足に「もっていくもの」、海に「もっていくもの」、山に「もっていくもの」。
それは「素材」とか、「ツール」とか、「道具」といった意味に近いものです。
もって行けば、見たいものがよく見えたり、知りたいことが、よくわかったりします。
黄金のLを、もって行かなくてもいいです。自分に合うものをもって行けばいいのです。
黄金のLを、途中で捨ててもいいです。新しい「ツール」を見つけたら、または自分で作ったら、ぜひ教えてください。
これから、「正五角形」を見に行きます。
そのとき「黄金のL(エル)」をもっていくと、どのように役立つか。3つあると思います。
1つ。黄金のL(エル)があれば、星形正五角形が簡単に書けます。・・・【第1部】
2つ。黄金のL(エル)がわかれば、いろいろな正五角形の作図法が分析できるようになります。そして複雑な数式を使わなくても、なぜ正五角形になるのかという作図の意味がよくわかるようになります。・・・【第2部】
3つ。黄金のL(エル)を使いこなせるようになると、黄金のLを素材として、自分の力で新しい正五角形の作図法をつくり出すことができるようになります。ぜひ挑戦してください。・・・【第3部】
【第1部 星形正五角形の簡単な書き方】

黄金のL(エル)があれば、星形(正五角形)は簡単に書けます。
定規とコンパスを使います。

まず、黄金のLの書き方から始めましょう。
■黄金のLの書き方(その1)

横に線を引きます。
この水平線の左はしに直角をつくります。

コンパスの針を、水平線から少し離れた上の位置に置きます。
コンパスの芯は、水平線の左はしに置きます。

水平線から太陽が昇るような形で円を書きます。

円が水平線と右側で交わる点と、円の中心を通る直線を考えます。
この直線が円を横断し、反対側と交わる点に印しを付けます。

この印しと、水平線の左はしを通る直線を引くと、垂直線ができます。

これは、円に内接する三角形の一辺が、円の中心を通るとき、その三角形は、必ず直角三角形になるという性質を応用した作図法です。

このように、基本の作図である「垂直線の作図」を行う方法もあります。
黄金のL(エル)は、この直角を構成する水平線と垂直線を、黄金比の長さになるように整えたものです。
それでは、黄金比をつくって行きましょう。

コンパスの針を直角の部分に置き、コンパスの芯を垂直線の上に置きます。
その幅は自由です。これが基準の長さ(1の長さ)になります。

コンパスの芯を直角の部分に置き、コンパスの針を水平線の上に置き、半円を描いて、基準の長さの2倍を水平線の上に取ります。これは「黄金のL」のヨコ線の長さ(2の長さ)になります。

垂直線上の1の点にコンパスの針を置き、水平線上の2の点にコンパスの芯を置き、上へ弧を描いて、垂直線と交わる位置に印しを付けます。これは「黄金のL」のタテ線の長さ(1プラス、ルート5の長さ)になります。
※コンパスを開いた幅は、ルート5の長さになっています。

印しを付けた位置からはみ出た部分は、消しておきましょう。
■黄金のLの書き方(その2 正五角形の一辺の長さが与えられた場合)

正五角形の一辺の長さが与えられた場合は、その辺の2等分点を作図することから始めます。

2等分点が決まったら、2等分線上にコンパスの針を置き、一辺の左側にコンパスの芯を置いて、

先ほどの要領で垂直線を書きます。

直角の位置にコンパスの針を置き、一辺の2等分点に芯を置いたら、その長さ(1の長さ)を垂直線上に作図します。

次に、垂直線上の1の点にコンパスの針を置いたら、水平線(2の長さ)の右端にコンパスの芯を置きます。
この幅(ルート5の長さ)を垂直線上に重ねて取り、1プラス ルート5の点を作図します。

黄金のL(エル)の形である、「水平線の長さ2に対する 垂直線の長さ 1プラス ルート5」が作図できました。
■星形(正五角形)の書き方 その1
(正5角形の作図 1)

星形は、黄金のL(エル)から簡単に作れます。
黄金のLのヨコ線とタテ線の長さは、黄金比になっています。

定規とコンパスを用意します。

ヨコ線の幅にコンパスを開きます。
ヨコ線の左に針を置いて、

左に弧を描きます。(弧(こ)は円周の一部です)

つぎにヨコ線の右に針を置いて、

右に弧を描きます。

こんどは、タテ線の幅にコンパスを開きます。
ヨコ線の左に針を置いて、

右に弧を描きます。

つぎにヨコ線の右に針を置いて、

左に弧を描きます。

ヨコ線の左右2つの点と、4つの弧の3つの交点に印しをつけます。

その5つの点を結ぶと、正五角形、そして星形ができます。
もう一度やってみましょう。
黄金のL(エル)を、黄金の箱に例えましょう。
ヨコ線を小さなフタ、タテ線を大きなフタとしてみます。

コンパスの幅を小さなフタに合わせます。

左についた小さなフタを、左に開け、

それから右につけた小さなフタを、右に開けます。

こんどはコンパスの幅を大きなフタに合わせます。

左についた大きなフタを、右に閉じ、

それから右につけた大きなフタを、左に閉じます。

黄金の箱(黄金のL)から、星形が出てきました。
■星形(正五角形)の書き方 その2
(正5角形の作図 2)

黄金のL(エル)にはおもしろい性質があります。
いろんな大きさの円があれば、その大きさにぴったりあてはまる星形を書いて行くことができるのです。

こんどはその方法についてお話しします。

黄金のLのヨコ線は、正五角形の一辺の長さになっています。

黄金のLのタテ線は、星形の一辺の長さになっています。
※ これは、正五角形の対角線の長さでもあります。

黄金のLのタテ線とヨコ線の端をナナメに結ぶと、黄金直角三角形ができます。

黄金直角三角形の直角からナナメ線に垂直線を引きます。

すると、この垂直線の長さは、その星形(正五角形)がぴったりあてはまる円の半径になるという性質があります。
※ 星形(正五角形)の外接円の半径になります。

ここでできた小さな直角三角形は、

大きな直角三角形と同じ形をしています。
※ 3つの角が同じ相似形です。

小さな直角三角形のナナメ線が正五角形の一辺の長さであるとき、タテ線は正五角形がぴったり当てはまる円の半径になっていました。

ですから、大きな直角三角形のナナメ線が正五角形の一辺の長さであるとき、タテ線は正五角形がぴったり当てはまる円の半径になるのです。

好きな大きさの円を描き、

その半径を、黄金直角三角形の頂点からタテ線上に取り、

そこから黄金直角三角形のナナメ線へ垂線を引き、

垂線とナナメ線が交差する位置から、頂点までの長さに、コンパスの幅を開くと、


コンパスを使って、円周を5等分する点を円に付けることができます。

もう一度やってみましょう。

いろいろな大きさの円があっても、

同じ大きさの黄金直角三角形の頂点から、

その半径を、タテ線上に取り、

そこからナナメ線へ垂線を引き、

垂線とナナメ線が交差する位置から、頂点までの長さに、コンパスの幅を開くと、





コンパスを使って、円周を5等分する点を円に付けることができるので、


いろいろな大きさの星形(正五角形)を描くことができます。
5等分点をつける方法は、いろいろと工夫できます。

これは、コンパスの軸(針)の位置が4カ所あります。白抜きの部分です。

これは、コンパスの軸(針)の位置が3カ所あります。
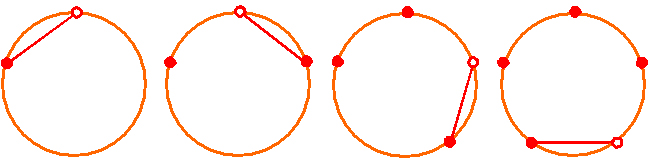
これも、コンパスの軸(針)の位置は3カ所です。自分が好きな方法で作図してください。
【第2部 いろいろな正五角形の作図法の分析】
第2部を理解すると、いろいろな正五角形の作図法のポイントが分析しやすくなります。そして複雑な数式を使わなくても、なぜ正五角形になるのかという作図の意味がよくわかるようになります。
黄金のL(エル)に注目してください。
■黄金比と黄金のLの詳しい説明
黄金のL(エル)は、直角を構成する長いタテ線と短いヨコ線が、黄金比になっているものです。
黄金比は、長い部分が1プラス ルート5であるとき、短い部分は2になります。
いまから黄金のLを作図します。
どこに黄金のLができたか、また、いくつできたか、ご確認ください。

水平線の上に正方形を置きます。その一辺の長さを2とします。

正方形をタテに2等分する線のいちばん下に、コンパスの針を置いて、

正方形の右上までの長さを、コンパスの幅で取ったら、

水平線まで右に弧を描きます。

このとき、黄金のL(エル)は2つできています。

黄金のL(エル)は、ここと、

ここです。

小さなL字形が、本当に黄金比になっているかどうか、確かめてみましょう。
黄金比は、2 対 1プラス ルート5 でした。
比は分数でも表すことができるので、これは、
と表すことができます。
これは大きな黄金のLの短い辺と長い辺の、長さの比率を表しています。
小さな黄金のLについても、同じように分数で表すと、
になります。
分数で、分子と分母が同じものは、どんなに複雑な数式でも、「1」になりますから、分母と分子が同じになるような数式を掛けてみます。

計算を進めてみましょう。

小さな黄金のLの比率を計算すると、黄金比を分数で表した、2分の 1プラス ルート5 になることがわかります。
これは黄金比の重要な性質で、

黄金のL(エル)の短い辺に、それと同じ幅の正方形を書くと、

黄金のLの長い辺の余った部分に、小さな黄金のLができます。

この余った部分と同じ幅の正方形を書くと、さらに小さな黄金のLができます。
これはどこまでも続きます。
正五角形の作図では、小さな黄金のL(エル)に注目すれば、なぜ次の方法で正五角形が作図できるのか、その理由がはっきりすると思います。

円が与えられたら、それを4等分する左上の部分に、正方形が重なる様子を思い浮かべます。
そして小さな黄金のL(エル)を作る方法について考えます。

上下左右の円周上に、4等分する点を取り、

左右を通る水平線上に、半径を二等分する点を取り、

そこから上の点までの幅を、

水平線上に降ろします。

こうしてできた黄金のL(エル)の両端を、

ななめに結んだ線の幅を、コンパスで取ります。

この幅は、円に内接する正五角形の一辺の長さに相当するので、

円周を、五等分することができます。
■黄金のLと正十角形との関係
次に、黄金のL(エル)と、正十角形の一辺の長さとの関係についてご説明しましょう。ここから別の種類の作図法が生まれます。
半径2の円に内接する正十角形の一辺の長さ(ルート5マイナス1)は、すでに先ほどの黄金のLの短辺(底辺)の長さとして表示されています。
まず、この図をご覧ください。

正五角形の中にできる黄金二等辺三角形は、頂点が円周上にありますが、正十角形の中にできる黄金二等辺三角形は、頂点は円の中心にあります。

正五角形の一辺と対角線を直角にして黄金のLをつくり、それに斜辺を付けた黄金直角三角形の直角から斜辺へ引いた垂線の長さは、正五角形が内接する円の半径に等しくなります。
正五角形と同じ円に内接する正十角形を見ると、円の半径は黄金二等辺三角形の斜辺の長さです。
共に黄金比の長い部分を構成する斜辺と垂線の長さは等しいので、黄金二等辺三角形の底辺と、黄金直角三角形の中にできる小さな黄金のLの底辺の長さは等しくなります。

ですから、大きな黄金のLの底辺が、正五角形の一辺の長さであるとき、小さな黄金のLの底辺は、同じ大きさの円に内接する正十角形の一辺の長さになるという関係があるのです。

黄金のL(エル)から作られた黄金直角三角形の三つの辺の関係を、図を用いて確認しましょう。
Aは、正五角形と正十角形の外接円の半径です。
Bは、その円に内接する正五角形の一辺の長さです。
Cは、その円に内接する正十角形の一辺の長さです。

半径2の円に内接する正十角形の一辺の長さは、先ほどの作図法から見ると、ルート5マイナス1であることがわかります。

水平線上の半径2分の1の点にコンパスの針を置き、ルート5の間隔に開いて弧を描いた作図を逆にたどると、上の点とを結ぶ斜線上に、正十角形の一辺の長さが作図できることがわかります。
それでは、正十角形の一辺の長さによる正五角形の作図を始めます。

先ほどと同じように上下左右の円周上に、4等分する点を取り、

左右を通る水平線上に、半径を二等分する点を取り、そこから上の点まで線を引きます。

半径の二等分点にコンパスの針を置き、円の中心にコンパスの芯を置いて間隔1の幅を取ったら、その線まで弧を描きます。

弧と直線との交点から、円の上の点までの幅をコンパスで取ります。これが正十角形の一辺の長さである、ルート5マイナス1の長さになります。

円のいちばん下の点にコンパスの針を置いて、左右両側に正十角形の一辺の間隔を取ります。

その左右の点を結ぶと、正五角形の一辺の長さが求まります。コンパスをその幅に開いて、円周上の左右上側に点を付けます。

正十角形の一辺の長さ(小さな黄金のLの底辺の長さ)を使って、星形正五角形が作図できました。
【第3部 新しい正五角形の作図法】
第2部では、正五角形の作図法を分析するために、代表的な2つの作図法について、黄金のLを中心にご説明しました。
第1部の作図法と、第2部の2つのポイントを押さえたら、星形正五角形は、まるでパズルを組み立てるように、工夫しながら自由に書くことができるでしょう。
第2部の2つのポイントを、もう一度確認しておきましょう。

上下に並んだ2つの黄金のL(エル)に、3つの円を書くと、円周の5等分点を作図することができます。この2番目と3番目の円が、その2つのポイントです。
どうぞ新しい工夫で、あなたの作図法を作ってみてください。
【補 講】
やさしい星の書き方として、正五角形のほかに、正六角形、正八角形の書き方の一例をご紹介しましょう。
■星形(正六角形)の書き方

(正6角形の作図)

(1) 円を書きます。


(2) コンパスの幅はそのままで、円周上に印しを付けて行きます。すると円周を6等分する点を付けることができます。

(3) 円周上の6つの点を結ぶと、正六角形と星形正六角形ができます。
■星形(正八角形)の書き方

(正8角形の作図)

(1) 円を書きます。

(2) 円の中心に定規を合わせ、円の左右に点をつけます。


(3) コンパスの幅を広げ、左右の点を軸に上側に半円を書きます。半円は中央で交差するようにします。

(4) その交差した点と中心点に定規を合わせ、円の上下に点をつけます。

(5) 上の点を軸に上側に、前と同じ幅で半円を書きます。そのとき2つの半円と重なるようにします。


(6) 半円の交点と円の中心に定規を合わせ、円周上に左上と右下の点、そして右上と左下の点をつけます。


(7) 円周上の8つの点を結ぶと、正八角形と星形正八角形ができます。
【おわりに】
いかがでしたでしょうか。
次回は、定規とコンパスを使った「星形正九角形」の作図を予定しています。
物語「教材作家」第23話では、「三乗技法」という立方根の作図法についてお話ししました。
正九角形の作図法としては、コスモ定規という特殊な定規を使った作図法を第13話でご紹介しましたが、次回は「三乗技法」と同じように、普通の定規とコンパスでできる「角の三等分技法」を使った作図法についてお話しします。
2009年10月28日 川内尋嗣(手作り教材くらぶ)
☆☆☆☆☆ 「角の三等分問題 ミトブ法と正九角形の作図」を公開しました(2011年12月1日)
【関連資料】
黄金比の直角三角形の垂線と正五角形の外接円の半径 (教材作家 第7話)