教
材
作
家
<第15話> KS論分科会 〜円積問題と平方根の作図〜
「あ、おにぎりおばちゃんだ」
KS論基調講義のあと一時休憩となり、浜崎が校舎の外へ出て来ると、三人の女の子たちが顔を上げた。
「あら、ウサギを飼ってるのね。名前は何ていうの?」
「ハナ」
「白ウサギだから、白い花というわけね」
「ちがうよ。はな」
トモミが自分の鼻に指を当てて答える。
「この子、いつも鼻をひくひくさせているの。だからハナちゃん」
「ああ、そのハナちゃんね」
浜崎の後に続いて出てきた佐藤が、遠くから歩いてくる波木に呼びかける。
「会長! こちらです」
波木がゆっくり歩きながら浜崎に説明する。
「新しい工場には、装置の設置義務はないと、工場側は言っているわけです。その件については平和台村役場も承認済みだと・・・」
「ひどい話ね」
「我々は、教材クラブとして、工場側に汚染物質除去装置の設置を要請するつもりです。
その技術的なことについての説明や見積りについて、信頼できるメーカーにお願いしたいのですが、浜崎さんのお知り合いに、そういう方がいらっしゃるのですね?」
「ええ。私の甥っ子がメーカーに勤務しております。そういう機械を最近扱ったと聞いております」
「それは好都合だ。ぜひ平和台村に来ていただいて、工場側も交えた席で、お話を伺いたいのです」
「わかりました」
佐藤が口をひらく。
「会長、具体的な話は、第二分科会でお願いします。みんなの同意の上で進めたいと思いますので」
「当然だ。浜崎さん、ご一緒によろしいですか?」
浜崎はうなずくと、彼らと一緒に教室へ戻りはじめた。
波木がいう。
「浜崎さんは、この小学校を卒業されたそうですね。平和台へはよく来られるのですか?」
「何年かに一度、同窓生に会いに戻って来るのです」
「そうですか」
波木が佐藤に訊ねる。
「第二分科会には何人くらい集まっている?」
「10名ほど」
「そうか。少ないな」
「当初の予定は、第一分科会の"教育について"だけでしたから。そちらの方へ30名近く集まっています」
「"工場建設について"という新しいテーマには、抵抗を感じている人も多いのだろう。村役場の意向もあるし…」
「教材クラブは政治的宗教的活動にたいして中立の立場を取らなければならないという、以前KS論で議論され承認された原則に忠実なのです」
「立ち退きを要求されていてもか?」
波木は立ち止まって佐藤を見るが、また思い直したように歩きはじめる。
「…いや、もう言わないことにするよ。教材作家は一人一人考えが違って当然だ」
「ところで健一君はどうした?」
「彼の提案で、"教材作家の方法"をテーマに、第三分科会がつくられました。5名ほど集まっています。
デロスの問題の具体的な解決策へ近づこうとするものです」
「第二分科会も、健一君がつくったようなものだ。
彼がデロスの問題を引き受ける前は、教材クラブは、工場建設に関する活動は禁止されていた。
彼がデロスの問題を引き受けたので、教材クラブは工場側との契約の当事者となることができた。
この当事者としての立場を利用して、我々は工場側に新たな提案を行う。
汚染物質除去装置の取付け要請だ。
工場側が装置の取り付けを了承すれば、我々はただちにここを立ち退く。
そうなれば、教材まつり三日目は別の会場で行えばいい。
そのときデロスの問題に関する講義は、新しい解決策でなく、"水測法"の講義で十分なのだ。
このことは、健一君は知っているのかな?」
「いえ、まだです。高山君に説明させます」
「彼はいったん東京へ帰るのだろう?」
「そのようです」
休憩時間が終わり、三つの分科会がそれぞれ始まった。
第三分科会には、高山と健一、美奈子、そして内田と山中が参加している。
まず最初に高山が話しはじめる。
「教材作家が一人いれば、一つのKS論が生まれる。
健一君が知りたい教材作家の方法は、教材作家の数だけあるだろう。
速見さんや、我妻さんが話したことの中にも、教材作家の方法があった。
現実の問題に、自由な発想で挑む、問い掛ける。
問題自体も、与えられた問題にとらわれることなく、自由に自分で作ってみる。作りかえてみる。
自由に問い掛け、その問い掛けに自由に答える。
さらにその答えを契機として、新しい問い掛けが生まれる。
新しい問い掛けは、新しい希望、新しい出発点だ。
その問い掛けに、さらに新しく自由に答えようとする。
この繰り返しによって、問い掛けの質が、らせん状に上昇して行く。
問い掛けの質や自由度を、どれだけ高められるか。
教材作家はそのために、一人一人違う流儀や、日常生活上の工夫というものを持っている。
教材作家にとっての答えとは、その中にあるということだ」
健一がいう。
「問い掛けの質や自由度を高めれば、必ず答えが見つかるという保証がありますか?」
「保証だって?
君もさっき言ったじゃないか。
教材作家は問い掛けを重視する。答えは強く求めないって。
自分が本当に納得のいく答えが見つかるかどうかは、人との出会いと同じ、ご縁みたいなものだというのが僕の考えだ」
「もし納得のいく答えに出会えなかったら?」
「一生問い続けるしかない」
「死ぬまで問い続けるなんて、死ぬときまで最終の答えが出ないなんて、そんなの耐えられるのでしょうか」
「そんなに答えが知りたいのか」
「知りたいです。みんな答えを知りたがっているはずです」
「そんなに早く答えを知りたい人間は、ここへは来ない。すぐ答えを与えてくれるところへ行くさ。でもなあ・・・」
「でも、何ですか?」
「そんなに簡単に出た答えが、何の役に立つんだ?」
「インターネットで検索すれば、答えは早く見つかりませんか?」
「そりゃあ、見つかるさ」
「その答えは、役に立たないのですか?」
「・・・あのね、その答えは自分の答えじゃあない。他人の答えだ。他人の生きた経験、実践の結果を、文字にしたものだ。」
「答えに、自分のもの、他人のものといった区別があるというのですか?
真理は、人間から独立して存在しているのではないでしょうか」
「君が言っている真理という言葉は、君から独立しているのかね。
君が考えたり、しゃべったり、書いたりする言葉は、君から独立して一人歩きはできないのだ。
君の言葉は、君の生きた経験、実践の結果。他人のそれとは違うものだ」
高山は首筋まで真っ赤にして言う。
「他人と同じ考えを持つと思うなら、証明してみることだ。
自分の生きた経験、実践の結果、他人と同じ結論に至ったら、それは君の答えだ」
健一は、高山の大声を前に、何もしゃべれなくなってしまった。
「おい高山君、だいじょうぶか」 第二分科会の方から佐藤が声をかける。
周囲の驚いたような視線に気がついた高山は、冷や汗をかいたような表情を浮かべた。
「だいじょうぶです。すみません」
第一分科会に参加している30名近い教材作家たちが、中断した"教育について"の議論を再開した。
教室の入り口から中を窺っていた若い女性が、高山の居場所に気づいて入って来ると、か細い声で話しかけた。
「"星座のうた"の合奏の練習、だいぶ進んでいるから、子供たちを見に来てあげて」
「ああ、そうか。わかった。あとから行くよ」
高山はハンカチで顔をぬぐいながら言う。
「雅恵、ちょっと来てくれ」
第二分科会の集まりの中にいた副会長の佐藤が、その平和台小学校で音楽の教師をしている娘の雅恵に声をかけた。
雅恵はうつむき加減に佐藤の方へ歩いていく。
高山の大声が気になったのか、第二分科会に参加していたゲンが立ち上がり、雅恵と入れ替りにこちらへ来ると、健一の近くの椅子に座った。
第三分科会に参加した教材作家の一人、内田が話し始める。
「"不可能を可能にする教材作家の考え方"と健一君はいうけれど、そういう考え方のために、受験勉強を重視する親たちの中には、教材作家の教材は安心して子供に与えられないと思っている人もいる。
それは、教材作家が、学校では不可能だと教えられていることを、実用的には可能だと言うことがあるからさ。
教材作家が不可能を可能にできたと言うときのカラクリは、この実用的可能ということにあると思う」
「学校で使われている教材は、

ふつう、授業で教えられる範囲内にある。
でも、教材作家の教材は、子供たちに学ぶ楽しさを伝えるためならば自由に考えていいから、

授業の範囲から、外へ出ることもある」

「数学的に不可能と教えられることも、この外の範囲に出ると、実用的に可能になることがある。
正七角形の作図法も、円積問題で使う"パイ座標"もそうだし、デロスの問題だって水測法による2の3乗根の作図を考えるなら、この実用的可能の範囲にあるだろう。
しかし、学校のテストや入学試験などで、"可能です"と書くと、間違いになる。
受験勉強では、問題を見たら反射的に瞬間的に答えを出すような訓練がされる場合がある。
これは暗記力が試される試験では必要な訓練だ。
そういう訓練ばかりを重視する親たちは、試験場でそのまま書くと間違いとなる教材作家による解法が子供たちの知識の中に紛れ込んでいると、試験で大失敗をやってしまうと考えているようだ」
高山がいう。
「ほとんどの教材作家は、第一分科会に集まっているけれど、内田さんがいま言ったような内容について議論しているんだ。
そこでは、教育について一般論を述べ合う。
教材クラブには教師もいるし、父兄も、一般の人もいる。でもここに座ったら、立場は同じ教材作家だ。
学校の先生も、生徒の親も、自治会の人も、ここではそれぞれの立場を離れて、一人の教材作家として発言する。
この日のために、みんな教育についていろいろと研究してきたと思うよ」
もう一人の教材作家、山中が言う。
「受験勉強に役立たないとか邪魔になるとか、そう言う親たちは、ちょっと誤解しているんじゃないかなあ。
教材作家は物知りとは違う。子供たちが質問してきたら、子供と一緒になって頭を抱えているのが本当の教材作家だ。
子供たちが教材クラブに来るのは、答えが知りたいからではなく、一緒に考えてくれる大人が必要だからだ。
教材作家だって、子供たちの自由な発想を知りたい。
安藤さんのパイ座標だって、安藤さんに聞いてみると子供たちとの合作のようなものだ。
パイ座標と実際の円周率との誤差を、ウォーキングで歩こうと安藤さんが言い、子供たちはその距離をどうしても縮めたくて知恵を絞った。その子供たちの発想に刺激を受けて、安藤さんの教材はさらに成長を続けている。
教材の成長を契機として、子供も大人も成長できる。
教材クラブの意義はそこにあるので、受験勉強に役立たないとか何とか、どうしてそんなこと言うんだろう」
高山がいう。
「皆さん、申し訳ないが、子供たちが合奏の練習をしているので、中座させてもらいます。
内田さん、健一君の立方体倍積問題の参考にもなるだろうから、安藤さんのパイ座標について予習しておくというのはどうだろう」
健一もいう。
「内田さん、ぜひお願いします」
内田が頷く。
「わかった。はじめるよ」
高山が教室を出て行く。
内田は横に移動式のボードを用意すると話し始めた。
「午後の教材講義では、安藤さんによる円積問題についての教材講義がある。
安藤さんは、パイ座標という教材を書く。それはこんな形をしている。

一見なんでもないようだけど、数学的にはでたらめな座標だ。
なぜかというと、この図はパイを、座標上の位置として表している。
パイが " 3 " や " 3.14 "、それに " 7分の22 " や " 113分の355 " のように分数で表すことができる数であるなら、こういう図を書くことは数学的に可能だ。
分数で表すことができるためには、分子を分母で割ったときに割り切れる"有限小数"か、繰り返す"循環小数"でなければいけない。しかしパイはそのどちらでもない無理数だ。
パイが通常の無理数のように方程式の答えになれば、こういう図を書くことは数学的に可能だ。
" (ルート2)プラス(ルート3) " のように座標軸上の位置として、あるいは線分の長さとして書くことが可能になるから。
しかしパイは方程式の答えになることができない超越数だとされている。
ところで平方根の作図法を憶えているかな?
あとで重要になるからまとめておこう。
たとえば、(ルート95)の作図について考える。
(ルート95)という数は、面積95の正方形を考えたときに、その一辺の長さとなる数だね。

95という数は、5と19からできている。5×19=95だ。
座標を用意して、原点から左へ5、右に19を取る。

パイ座標もそうだけど、ここでいう座標上の点は、原点から上下左右への距離を示している。
だからマイナスの考え方はないよ。
原点を挟む5と19の中心を、コンパスを使って求めたら、

そこから5までの長さを半径とした半円を書いてみる。

半円とタテ軸との交点が、原点からの距離(ルート95)を示す。

一般化してabで考えてみよう。

(ルート2)は、a=1、b=2として作図する。
(ルート3)は、a=1、b=3として作図する。
(ルート10)は、a=2、b=5として作図する。
(ルート21)は、a=3、b=7として作図する。
(ルート31)は、a=1、b=31として作図する。
(ルート95)は、a=5、b=19として作図する。
abは逆でもいいよ。
そして、(ルートパイアール2乗)は、a=アール、b=パイアールとして作図する。
さて、話を円周率(パイ)に戻そう。
身長1メートルの子供と同じ背の高さの車輪が、1回転したときに進む距離をパイメートルという。

これを3.14メートルとか、3メートル14センチ1ミリ半と答えるのは、技術的には正しいけれど、数学的にはパイメートルが正しい。
座標軸上でパイは、3に近く、3.14にもっと近い。
座標軸上でパイは、3.141592にもっともっと近く、3.14159265358979にもっともっともっと近い。
限りなく近づくことはできても、決して出会えない数、それがパイだ。
1991年に出版された金田康正氏の"パイのはなし"によると、パイの姿は10億ケタを越えている。
現在では1兆ケタを超えるところまで計算できていてまだ終わらないそうだ。
パイの大きさは3.14とほとんど同じだけれど、その姿は、1兆個の数字を並べてもまだ正確に表し切れない。
だから、パイの全貌を声に出して読んでみたいなんて思わない方がいいよ。
1兆個の数字を読み上げようとすると、1秒間に4個ずつ不眠不休で読み上げても、7900年以上もかかってしまうからね。
パイは○○に近いといえるだけで、小数でも、分数でも、ルート(根号)を使っても完全には表せない。
言葉を使って "パイ"と言うしかない、つまり数で表せない数だ。
0.33333…・という循環小数は小数の形では尽きないけれど、数直線上には3分の1という分数の部屋を持っている。
(ルート2)という無理数は、小数の形では1.41421356…・と尽きないけれど、数直線上には(ルート2)という無理数の部屋を持っている。
しかしパイには部屋がない。
円として書くと、あれほど完全に書けるのに、直線上に書こうとすると、原点からの位置が特定できない。
パイは数で完全には言い換えができない数なので、数直線上に表すことができない。
この付近にあると言えるだけだ。
コンピュータが発達する以前に技術計算で使われていた計算尺の目盛りには、数直線上にパイの位置が印されているけれど、これは技術的に許容できる誤差の範囲であり、技術的に正しいとみなされるからだ。
数学的にはパイの値を座標軸上に表すことができないので、"パイ座標"は書けない。
パイ座標が書けなければ、円と同じ面積の正方形も作図できない。
だから円積問題は解けない。
しかし数学的には書くことができない"パイ座標"が、"書けた"とすると、たちまち円積問題が解けてしまうんだ。
やってみるよ。
十文字の座標の右上に、傾きパイの直線を書く。

その下に、座標のタテ軸ヨコ軸に接するように好きな大きさの円を書く。

円の中心から、傾きパイの直線まで線を延ばし、そこからさらにタテ軸へ垂線を引く。
ここへ青い点を付けよう。

円の中心からもタテ軸へ垂線を引く。
そこに赤い点を付けよう。

座標を右へ90度倒し、コンパスを使って青と赤の点の真ん中を求め、そこに黄色い点を付ける。

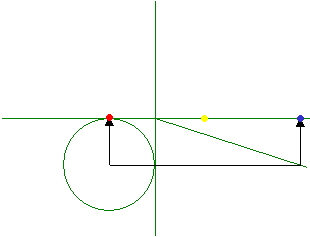
黄色と赤の点を結ぶ線の長さを半径とした半円を、黄色い点を中心として赤い点から青い点まで上側に書く。

半円と座標軸が交差した点から原点までの長さを一辺とした正方形を作図する。


座標を左へ90度戻してみよう。

円と正方形の面積は等しい。
円積問題の解答は、数学的に不可能であっても、技術的に不可能と決まったわけではないだろう。
数学的に不可能なことを、技術的に可能とするためには、誤差が実用化に問題を生じさせない範囲内であればいいからね。
宇宙規模で不可能であっても、地球規模で可能であればいいのだ。
これは数学者の考え方ではなく、技術者の考え方だよ。
直径1万キロメートルの円を考えてみよう。

1万キロメートルは地球の赤道から北極点までの長さで、地球一周の4分の1だね。
1万キロメートルの直線を考えて、その中心を軸として半回転させる。
直線の両端の通過位置に印をつけていくと円が書ける。
その円周の長さを、ミリ単位未満を切り捨てて言うと、
円周率(パイ)は、3.1415926535 と続いていくから、
3万1415キロメートル926メートル53センチ5ミリだね。
円周をパイ座標を使って求めてみよう。
パイ座標を、ヨコ軸に1、タテ軸に3.14を取って書いてみる。この作図には目盛り付き定規があった方がいい。1単位を10センチメートルとして書くよ。

パイ座標を延長して考えて、直径1万キロメートルの円周の長さを求めると、3万1400キロメートルとなる。

実際の円周より、パイ座標の値は、
10000×3.1415926535 −10000×3.14=15.926535
だから、約16キロメートル短くなる。
目盛り付き定規を使わない場合の手軽な作図法として、(ルート2)+(ルート3)があるよ。

教材作家の安藤さんは、パイ座標を、
タテ軸に分子の値、(ルート10)+(ルート21)+(ルート95)
ヨコ軸に分母の値、(ルート31)
を取って書いてみた。

ルート(根号)が付いた4つの数字は2ケタのものを選んである。これは、パイ座標を一般の定規とコンパスを使って無理なく作図できるようにするための工夫だよ。
ほら、ここに(ルート95)が出てくる。
タテ軸にこの長さを取ったら、その上に(ルート21)と(ルート10)の長さをつなぎ合わせ、その位置に印をつける。
ヨコ軸には(ルート31)を取って印をつける。
そして2つの印から垂線を伸ばし、その交点を通る直線を原点から引くと、傾きがパイに近い直線が作図できる。
その傾きは、分子を分母で割ってみると、3.1415926680 と計算できる。

このパイ座標を延長して考えて直径1万キロメートルの円周の長さを求め、実際の円周と比較してみよう。

10000×3.1415926535−10000×3.1415926680 = −0.000145
だから、パイ座標によって求めた値は実際の円周より、約14センチ5ミリ、ボールペン1本分だけ長くなる。
パイ座標の考えを宇宙空間まで広げていくと、その誤差はどんどん拡大していくから、パイ座標を使うことは数学的には誤りとなる。
しかし地球規模で考えると、直径1万キロメートル当りの誤差14センチ5ミリ、直径1千キロメートル当りであれば1センチ4ミリ半の誤差を差し引けば、技術的には誤差はゼロとなるだろう。
教材作家は、教材という物を作る職人、実用化をめざす技術者とも言えると思う。
数学者は宇宙規模で考えるから不可能だと言うかもしれないけれど、技術者は地球規模で可能であれば実用化を考えるだろう。
技術者は、数学者が算出した数字を理想とし、目標としながら、現在到達している技術レベルとの誤差をどれだけ小さくできるかを考える。
その工夫を思い付くのに、プロもアマチュアもないだろう。
今年の教材まつりのテーマ "ギリシアの三大作図問題"の基本となる考え方は、数学的に解答不可能とされた問題を、いかにして技術的に解くかということにあると思う」
「そうなると」 ゲンが内田を見る。
「デロスの問題についていうなら、2の3乗根に近い値を、実用化できる範囲で作図するのが教材作家の方法ということになりますね。
しかし2の3乗根の近似的作図に成功しても、工場側が納得すると思いますか?」
内田が答える。
「もちろん、2の3乗根の作図はパイ座標のような、実用的な近似的作図ではだめだろう。
正七角形の作図と同様、2の3乗根の作図は、機械的作図法によって誤差の問題が生じないということがわかっているからね」
健一が内田にいう。
「実用的可能な方法でデロスの問題を解こうとする場合、定規とコンパスだけで出来るのでしょうか?」
内田がいう。
「定規とコンパスの、通常の使用方法ではない使い方によって解く。それから・・・」
「教材ではない意外なものに教材性を見出して解く」 ゲンがいった。
「そう。その方法がある」 内田が頷いた。
ゲンは健一の方を向くと、こう言った。
「デロスの問題という正統な数学の方法では作図不可能な問題を、作図可能とする教材作家の方法には、三つあると思う。
教材まつりの"はじめのことば"で、波木会長が言っていた方法だよ。
一つ目は、新しく教材を作って解く。
二つ目は、教材の新しい使用法を見出して解く。
三つ目は、教材ではない意外なものに教材性を見出して解く。
使用できる教材は定規とコンパスだけなので、特殊な定規の製作や使用など、一つ目の方法は使えない。
残るは、使用法の発見か、教材性の発見ということになりそうだけれど、どうだろう?」
「ゲンさんの言う通りですよ」 山中がにこやかにいう。
「教材作家は教材の使用法にとらわれず、教材そのものにもとらわれない。
物の価値を決めつけず、限定せず、見限らず、常に新しい目で見ようとする。
赤ん坊の目のように、自分の目を、常に新しくしようと努力する」
「でも」 ゲンは少し薄笑いを浮かべて言った。
「期限は一週間しかないんですよ。健一君は具体的な解決方法が知りたいはずです」
健一が山中に訊ねる。
「山中さん、解答不可能な問題に答えた人の話って知っていますか?」
「僕に思い浮かぶのはね、一休さんの話とか、聖書の話かなあ」
「どういう話ですか?」
「屏風の虎退治の話だよ。
将軍が小坊主の一休さんに、屏風に描かれた虎が夜になると屏風から抜け出して人間に悪さをするから、その虎を縄で縛って捕らえよと命じる。
一休さんはわかりましたというと鉢巻を締めて縄を持ち、屏風の虎に向かって仁王立ちになる。
そして、 "さあ準備はできた。いつでも来い。どなたか虎を屏風から出してください!"と叫ぶ。
将軍は、大した知恵者だと一休さんを褒めたという話。
一休さんは、将軍が出した問題にそのまま答えてはいないところがポイントだ。
そのまま答えると、"それは不可能です"というのが答えになってしまう」
「それでは将軍の思う壺ですね」
「そう。似たような話が聖書にもあるんだよ。
イエスのもとへ、律法学者達が罪を犯した女をつれてくる。そしてモーゼの律法によれば、こういう女は石で打たなければならない。あなたならどうするか、とイエスにたずねる。
健一君はどう思う?
モーゼの律法に反せずに、その女を救うことは不可能な状態だ。
このままでは、女はイエスの目の前で殺されてしまうだろう」
「イエスがその問いに、律法に従って答えようとすると、石で打ちなさい、が答えとなるのですね」
「そう。でもそのようにはしない」
「どのように答えたのですか?」
「自分は罪深くないと思う人がこの女を石で打ちなさい、と言ったのだ。するとその場には、女とイエスを残して誰もいなくなってしまった」
「すごい答えですね」
「この二つの問題と答えを考えるとね、個別に起きた小さな問題がどんどん高められて普遍的な問題に発展し、その高いレベルの問題に、偉人達が答えているような気がするんだ」
「高いレベル?」
「答え方をみると、形式的には将軍たちや律法学者たちへの問いかけになっている。
一休さんは、"誰か虎を屏風から出してくれる人はいませんか?"と問い掛けている。
イエスは、"誰かこの女を石で打つことができるような罪深くない人はいませんか?"と問い掛けている。
この問い掛けは、実質的には、高いレベルの答えになっていると思うんだ。
"問い掛けの中に、答えがある"ということだ」
「その答えというのは?」
「そうだなあ・・・
一休さんであれば、"無理難題を民に押し付けて苦しめることはやめてください"という将軍への訴えになるかな。
イエスであれば、"自分の罪深さを自覚しなさい"という教えだろう。
それが、偉人たちがその問い掛けの中に秘めた主張であり、答えだと思う」
「問い掛けの中に、答えが含まれているなんてすごいですね。でも、実話なのでしょうか?」
「この人たちが、実際にそういうことをしたかどうかは重要ではないよ。
一休さんの逸話が江戸時代のものならば、その時代の人々の意識を、その中に読み取ることができるだろう。
重要なことは、我々の祖先たちがこういう考え方を人間の知恵として何百年何千年もの間、大切に受け継ぎ、語り伝えて来たということだ。
科学技術が発達するよりずっと前の時代から伝わる人間の知恵だよ。
教材作家は、もっともっとこういう昔からの知恵に学ばなければならない。
僕はそれが一番大事だと思う」
KS論が始まる一時間ほど前、別の教室では暗記カードゲーム、シャカルタ・リカルタの予選会の準備が始まっていた。
「シャカルタは教材作家の教材としては異質なの。それは受験対策用として高校生たちによって作られたからよ」
真理子がタケシに説明する。
「考案したのは、いま大学生になっている三年前の高校生たち。
その生徒たちは、暗記カードを友達と分担して作ろうとした。
そして、そのカードを持ち寄って、ゲームにして楽しもうとした。
楽しみながら学べる教材として、教材クラブ認定教材となったのよ」
教室内では高校3年生のシゲルが声を出し、10名の中学生高校生たちが彼に従って机や椅子の移動を行っている。
寒い朝に集まってきた生徒たちは、セーターなど厚手の服を着ているが、真理子だけは半袖の白いシャツに紺のスラックス、首には平和台中学陸上部顧問として使っている笛を掛けている。
作業中の生徒たちが小声で話す。
「マリッペ、あんな格好で寒くないのかなあ」
「鍛え方が違うんだってさ」
「シゲル!」
真理子に呼ばれ、シゲルが駆け足でやってくる。
「あと何名来るの?」
「予定では、ここにいるだけです」
「ええ?出場者は何名?」
「8名です」
「ベストエイトを決める予選会に、出場者8名なの?」
「…」
「タケシ!」
「はい!」
「あなた、何名つれて来れる?」
「あの…、健一はKS論に参加すると言っていました」
「何名かって聞いてるの!」
「さ、3名です」
「みんな集まって。
これじゃあ予選会を始められないでしょ?」
教室のドアが開き、厚いコートのポケットに両手を入れ、マフラーで鼻と口を覆ったトシオが、
「寒い寒い…」
と言いながら入ってくる。
腕組みをして立っている真理子と眼が合うと、トシオはそのまま回れ右をして出て行こうとする。
「トシオ!」
トシオの足が止まる。
「リョウスケは?」
「たぶん、まだ家で寝ていると思います」
「起こして来なさい」
「あいつ、夜遅くまで勉強して…それで…疲れて…」
「声が小さい!」
「起こして来ます!」
トシオは急いで出て行こうとする。
「みんな寝てるってわけ?」
トシオの足が止まる。
真理子が手招きをしたので、トシオは教室に入って来ると、他の生徒たちと並んで立った。
「10時に寝れば、5時に起きれるでしょ?
今はもう8時半よ。
みんな3名ずつ連れて来なさい。
いいわね?」
生徒たちはそれぞれ防寒服を身に着けると、足早に外へ出て行く。
コートのボタンがはずれたと言って手間取っている生徒に、他の生徒が小声でいう。
「おい、行こうぜ。早く行かないと、またマリゴンが火をふくぞ」
「何ですって?」
「行って来ます!」
予選会を取り仕切ったのが真理子でなかったら、生徒たちは休日の寒い朝にたたき起こされることもなかっただろう。
当初、出場者8名を含む12名だった参加者は、予選会が始まる時刻には30名に増えていた。
<第15話 終>