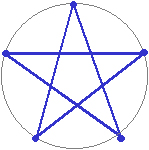
---

＜第５話＞　正五角形の作図　　〜黄金比の直角三角形による正五角形の書き方〜

「速見さん、これでいいんですか？」
健一が紙で作った直角三角形を速見にみせる。

「私もできました」
美奈子がハサミを置く。
「うん、それでいいよ。
紙とハサミがあれば、黄金直角三角形が作れたね。
僕が教育支援で教えている海外の子供たちは、コンパスのような高価な教材は使えない。
黄金直角三角形は、コンパスや定規がなくても作れるし、
紙に折り目を付けて丁寧に破ることができるなら、ハサミもいらない。
紙一枚あれば作れてしまうよね」

「健一君と美奈子さんに一枚ずつ黄金直角三角形を作ってもらったのには理由がある。
それは、正五角形の作図には、黄金直角三角形を二枚使うからさ」

「速見さん、糸を貰って来ました」
タケシが教室へ入ってくる。
その後ろから、真理子も入ってくる。「こんな糸でよかったかしら？」
速見は糸を引っ張ってみて、具合を確かめた。
「これでＯＫだ。伸び縮みしにくい、こういう糸がいいんだ。
この糸が、現地では円を書くためのコンパスの代わりになるんだよ」

「糸コンパスですね」　高山が言った。
「そうです。教材作家講義ファイルの中にあったものです」
速見は糸を結んで輪を作った。
「両手に一本ずつ鉛筆を持ち、輪に入れてピンと張る。
一方の鉛筆は動かないように固定し、
もう一方を、糸を緩めないように注意しながら動かす。
すると、円が書ける。
こんなふうに」

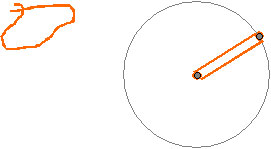
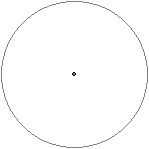
速見は、糸コンパスを使って、紙に円を書いた。
「正六角形の六つの頂点なら、糸コンパスだけで書けるよね。
糸がない場合は、指の長さくらいの長方形の厚紙を切って、両端に鉛筆を通す穴（合計２つ）を開ける方法でもいいよ。
この円は、後から使うので、ここに置いておこうね」

「さて、準備ができた。それでは・・・
黄金比の直角三角形による正五角形の書き方、・・・
そこで使用する教材の名前は、
"ゴールデンマスク（ＧＭ）"、つまり"黄金仮面"だ」

「黄金仮面？」
健一とタケシは、想像できないとでも言いたそうな表情だ。
「黄金直角三角形を、仮面の横顔に例えて書き方を説明するのさ」

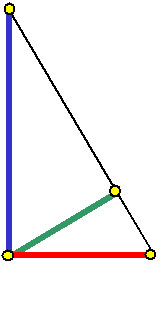
「まず、この黄金直角三角形の部分について、名前を憶えて欲しい。
左下に直角が来るような直角三角形を考える。
底辺を赤い線で書くよ。これをマウスライン（口の線）と呼ぶ。
底辺と垂直に立つ左辺を青い線で書くよ。これをヘッドライン（頭の線）と呼ぶ。
赤い線は短く、青い線は長い。
この長さの比は、"黄金比"になっている。
黄金比は紙が一枚あれば、子供でも簡単に作れるよね。
概略を説明するよ」

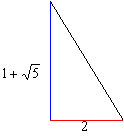
「直角をはさむ２辺の長さを１対２にとると、
その斜辺の長さは、ピタゴラスの定理により、ルート５になる。
ルート５の長さを、１の長さの辺に足して、1＋ルート５の長さにする」

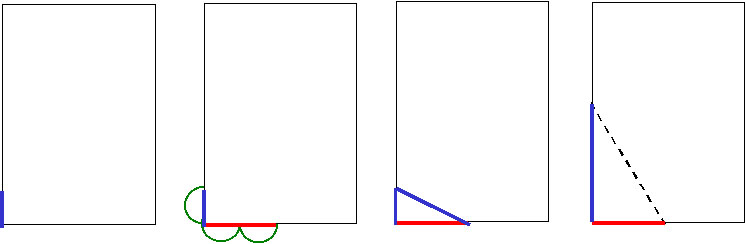
「健一君と美奈子さんに作ってもらったGMがここにある。
２　の長さの辺を、赤い色で表すよ。
１　プラス　ルート５　の長さの辺を、青い色で表すよ。
タケシ君には、作り方は後で説明するからね」

「赤いマウスラインの右端を、マウス（口）と呼ぶ。
青いヘッドラインの上端を、ヘッド（頭）と呼ぶ。
ヘッド（頭）とマウス（口）を結ぶ斜辺を黒い線で書くよ。
これをフェイスライン（顔の線）と呼ぶ」

「そして直角部分から、フェイスライン（斜辺）に垂線を引く。
この垂線を緑の線で書くよ。これをノーズライン（鼻の線）と呼ぶ」

「三つの角のうち、マウスとヘッドには名前をつけたけれど、
直角部分はまだだったよね。
直角部分は、フック（かぎ）と呼ぶことにしよう。
マスクの紐をつける部分だと考えてよ」

「イメージしやすいように、
目と鼻を書くこともあるよ。こんなふうに」

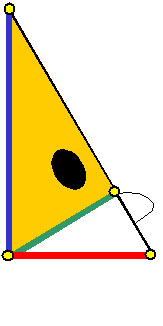
「この黄金仮面（ゴールデンマスク）は、二枚作っておく。
このとき、ノーズライン（緑の線）は省略して書かない。

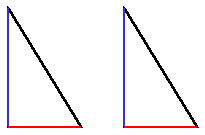
ノーズラインは落合クラブの勝本さんが見つけたとき、腰が抜けて動けなくなったくらい大事な線なんだけど、
小さな子供に説明するには難しすぎるからね」

「さあ、早速、正五角形を書いてみよう」

「まず、ＧＭ（ゴールデンマスク・黄金仮面）を、マウスラインを下にして置くよ。
フックとマウスの位置に印を付けて。
この点が正五角形の１番目と２番目の点になり、それを結ぶ線が正五角形の底辺になるよ」

「次は、三番目の点の位置を決めよう。
ＧＭが右を向くように、つまりフェイスラインが右にくるように二つのＧＭを並べてみよう。
ＧＭのフックが、それぞれ最初に付けた二つの印の所に来るようにしてみよう。
そして「ワン」と言ってみよう」

「それから、左のＧＭを、フックが印から離れないようにしながら、左に回してみよう。
そしてマウスラインが上を向いたら止める。
そして「ツー」と言ってみよう」

「そして、右のＧＭを、フックが印から離れないようにしながら、左に回してみよう。
右のＧＭの青いヘッドラインが、左のＧＭのマウスに当たったら、当たった状態のまま、
左のＧＭも、フックが印から離れないようにしながら、左に回す。
そして左のＧＭのマウスと、右のＧＭのヘッドが合わさったら、その位置に印を付ける。
そして「スリー」と言ってみよう」

「この点が、正五角形の三番目の点になるよ」

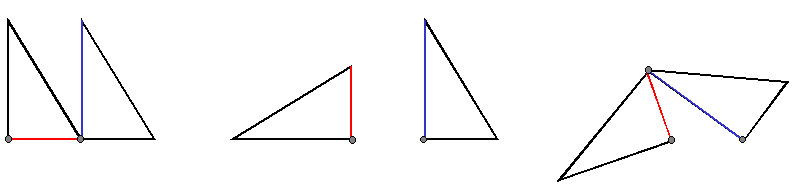
「次は、四番目の点の位置を決めよう。
ＧＭが左を向くように、つまりフェイスラインが左にくるように二つのＧＭを並べてみよう。
ＧＭのフックが、それぞれ最初に付けた二つの印の所に来るようにしてみよう。
そして「ワン」と言ってみよう」

「それから、右のＧＭを、フックが印から離れないようにしながら、右に回してみよう。
そしてマウスラインが上を向いたら止める。
そして「ツー」と言ってみよう」

「そして、左のＧＭを、フックが印から離れないようにしながら、右に回してみよう。
左のＧＭの青いヘッドラインが、右のＧＭのマウスに当たったら、当たった状態のまま、
右のＧＭも、フックが印から離れないようにしながら、右に回す。
そして右のＧＭのマウスと、左のＧＭのヘッドが合わさったら、その位置に印を付ける。
そして「スリー」と言ってみよう」

「この点が、正五角形の四番目の点になるよ」

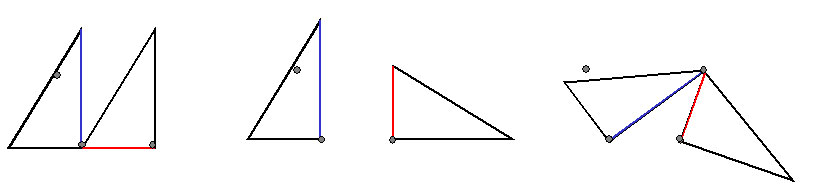
「最後は、五番目の点の位置を決めよう。
左のＧＭが左を、右のＧＭが右を向くように二つのＧＭを並べてみよう。
ＧＭのフックが、それぞれ最初に付けた二つの印の所に来るようにしてみよう。
そして「ワン」と言ってみよう」

「そして、左のＧＭを、フックが印から離れないようにしながら、右に回し、
同時に、右のＧＭを、フックが印から離れないようにしながら、左に回し、
そして左右のＧＭのヘッドが合わさったら、その位置に印を付ける。
そして「ツー」と言ってみよう」

「この点が、正五角形の五番目の点になるよ」

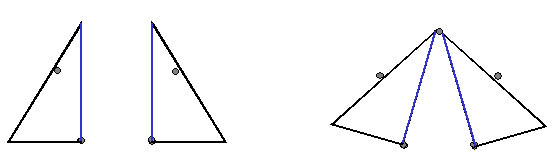
「五つの点を直線で順に結んだら、正五角形の完成だ」

「対角線を引いたら、星形正五角形の完成だ」

「いま述べた方法は、ゴールデンマスク（GM）を２個使う方法だ。
コスモ定規をコンパスのように回転させながら書く方法と基本は同じだね」

「次に述べる方法は、ゴールデンマスク（GM）を１個使う方法だ」

「ゴールデンマスク（GM）はすごい教材だよ。
どんな大きさの円を書いても、その半径より長いヘッドラインを持つGMがあれば、
その円に内接する正五角形が簡単に書けてしまうんだ」

「現地の子供たちは、コンパスを持っていないから、・・・
糸と二本の鉛筆を使って、・・・
こんな風に、円を書く。
先ほど書いた円と同じ円が書けた。同じ糸コンパスを使ったからね」

「さあ、タケシ君も、僕と同じようにやってみて。
先ほど書いた円は、・・・そこにあるね。
もう一つのGMを左手に持って、・・・
準備はできたね」

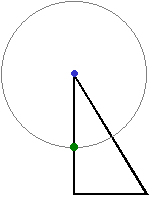
「さあ、はじめるよ。
まず、GMのヘッドを円の中心に当てて、円の半径の長さを、GMのヘッドライン上にとるよ。
緑の印をつけてみよう」

「その点から、ヘッドラインに対して垂直な線を引くことを考えて、・・・
その線とフェイスラインが交わる位置に赤い印をつけてみよう」

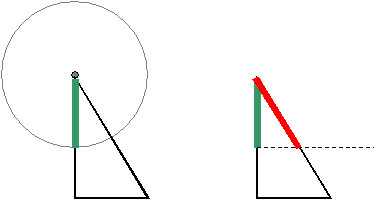
「具体的な方法は、・・・
緑の点でＧＭを二つ折りにする。・・・
ヘッドラインが重なるように」

「そしてまたＧＭを開いて、・・・
この折り目がフェイスラインに届いた位置に、赤い点をつけるよ」

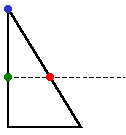
「わかりやすいように、ヘッドと緑の点を、緑の線で結んだよ。
そしてヘッドと赤い点を、赤い線で結んだよ」

「実は、赤い線を正五角形の一辺の長さとするとき、
緑の線は、正五角形に外接する円の半径に等しいんだ」

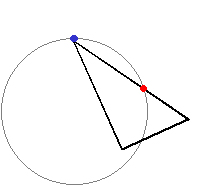
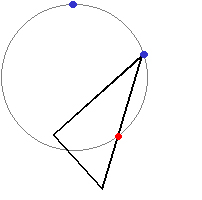
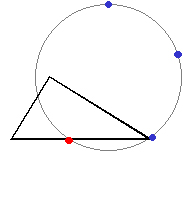
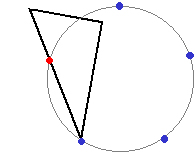
「ヘッドラインを半径とする円周上に、対応するフェイスラインの間隔で印を付けていくと、
円に内接する正五角形が簡単にできる」

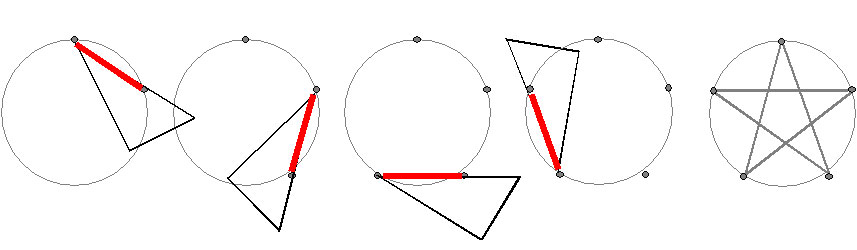
「これは、世界の国旗を書くときなどに、とても便利な方法だよ」

「旗の表面に、書きたい星の大きさを、
まず、円で印をつけておいて、・・・

ＧＭでその半径を測って、一辺の長さを求めたら、・・・

正五角形の頂点に次々に印をつけていけばいいんだ」

「あとは定規を使って、頂点を対角線でつないでいけば、星形正五角形の完成だ」

「さて、"直角三角形による正五角形の書き方"と僕が名づけた講義の最後に、
"ゴールデンマスク（ＧＭ）"、つまり"黄金仮面"の作り方を説明しよう」

「作り方は、簡単。紙が一枚あれば、あとはなにもいらない。
でも、正確に作ろうとするならば、定規とコンパス、はさみなどを使ってね」

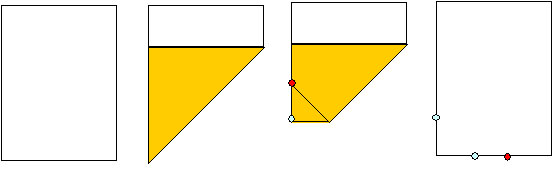
「まず、一枚の紙を用意して、・・・
下の辺が左の辺に重なるように三角に折って、・・・
左下の鋭角を上向きに折り曲げる。
鋭角が届いた位置に、赤い印をつけるよ。赤い印の位置で折り目をつけるだけでもいいよ。・・・
紙を開いてみよう。
折り目の位置が二つできているよ。タテとヨコに、直角からの距離は同じだね。
直角からヨコに、折り目の位置までの距離を２倍した位置に、赤い印がついているよ」

「さて、次は、直角からタテに伸びた左の辺を、直角からヨコに伸びた下の辺を横切るように重ねることを考えるよ。・・・
二つの辺を横切るように重ねる様子は、二つの道路が交差点で重なる様子と同じだね。
まず、直角からタテに伸びた左の辺を、先ほどの折り目で右下向きに折り曲げて、・・・
そのままその辺が先ほどの赤い点を交差点として、下の辺を横切るように重ねる。
交差点の位置に、青い印をつけるよ。青い印の位置で折り目をつけるだけでもいいよ。」

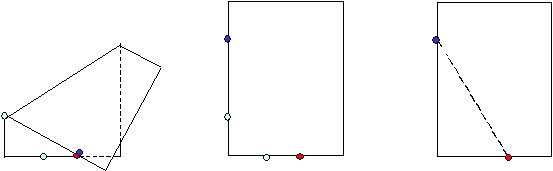
「直角からタテの折り目までの長さは、１　だね。
直角からヨコの赤い点までの長さは、２　だね。
タテの折り目からヨコの赤い点までの長さは、ピタゴラスの定理を使って計算すると、　ルート５　だね」

「紙を開いてみよう。
赤い点と青い点に注目して。
直角からヨコの赤い点までの長さは、２　だね。
直角からタテの青い点までの長さは、１　プラス　ルート５　だね。
この　２　対　１　プラス　ルート５　のことを、"黄金比（おうごんひ）"というね。
さあ、あとは赤い点と青い点を直線で結んで切り取れば、
"ゴールデンマスク（ＧＭ）"、つまり"黄金仮面"のできあがりだよ」

「さて、まとめてみよう。
星形正五角形を考えたときに、
ＧＭの赤い線は、一辺の長さ（正五角形の一辺の長さ）
ＧＭの青い線は、対角線の長さ（星形正五角形の一本の線の長さ）
ＧＭの緑の線は、外接円の半径に等しい。
ヘッドライン（青）とフェイスライン（黒）の長さの比は、
ノーズライン（緑）とマウスライン（赤）の長さの比に等しいという関係があるよ。
それらの辺により構成される二つの直角三角形は相似形だね」

「この講義は、これでおしまいです」

健一とタケシ、美奈子と高山、そして真理子は、
速見の講義に拍手で応えた。

「高山先生」　速見が言った。
「ノーズラインの説明は駆け足だったのですが、・・・
星形製図器（鉛筆孔付のＧＭ）の発表者である落合クラブの勝本さんは、
この垂線（ノーズライン）を見つけるまで何ヶ月もかかったと聞いています。
大変だったそうですね。」

「そうらしいですね」高山が言った。
「以前、勝本さんのお宅に伺ったときに、勝本さんから直接話してもらったのですが、・・・
この垂線が外接円の半径だという"都合のいい"仮説を立てるまでに長い時間がかかり、
そしてそれを証明しようとしても、方程式の立て方に誤りがあり、そして方程式の計算にも誤りがあって、なかなか答えが出なかったそうです。
いっその事、近所の高校生に手みやげを持って行って"僕はこう考えるんだけど、計算してみてくれないか？"と頼んだほうが早かったかもしれない・・・
後からそのようなことを思ったそうです」

速見は健一とタケシを見た。「君たちは現役の高校生だから、勝本さんが何度も間違ったという方程式とその計算はできるかな？」
「え〜？」タケシは頭を抱えた。
「その問題というのは・・・？」健一は恐る恐る訊いた。

速見がいう。
「では問題を言うよ。
二つのゴールデンマスク（ＧＭ）を使って正五角形を書くと、
ＧＭの赤い線の長さは、正五角形の一辺の長さに等しく、
ＧＭの青い線は、正五角形の対角線の長さ（星形正五角形の線の長さ）に等しい。
このときＧＭの直角から斜辺へ引いた緑の線の長さは、この正五角形に外接する円の半径に等しい、
と考えるがどうだろう。
同じ考えの人は、証明してみてください」

「さあ、二人とも頑張って！」真理子が元気よくいった。

＜第５話　終＞

【関連資料】　コンパスを使った星形の作図★★★やさしい星の書き方　正五角形と黄金のＬ（エル）（第１回　教材ファイル）